先看看反素数

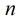
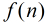
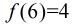
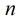
反素数的定义：对于任何正整数，其约数个数记为，例如，如果某个正整数满足：对任意的正整

            数，都有，那么称为反素数。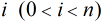　　

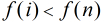
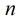
从反素数的定义中可以看出两个性质：

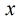
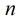
（1）一个反素数的所有质因子必然是从2开始的连续若干个质数，因为反素数是保证约数个数为的这个数尽量小

（2）同样的道理，如果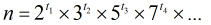，那么必有

根据这两个性质递归求解

线段树模拟叶子节点表示区间剩余的人的个数

#include
     
      #include 
      
       #include 
       
        #define lson l, m, rt<<1#define rson m+1, r, rt<<1|1using namespace std;int pri[20] = {
   0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,51};typedef long long ll;const int MAXN = 500008;int sum[MAXN<<2];int n, k;ll mxt, ord;int pos;void get(ll num,int idx,int cnt,int lmt)//num代表当前值，idx当前的素数，cnt约数的个数，lmt指数限制{    if(num > n) return;    if(cnt > mxt || (cnt == mxt && num < ord))    {        ord = num;        mxt = cnt;    }    int p = 1;    ll tmp = num;    while(p <= lmt)    {        tmp *= pri[idx];        get(tmp, idx+1, cnt*(p+1), p);//为什么是 p，为了是前一个素数的指数大于或等于后一个素数的指数        p++;    }}void buil(int l, int r, int rt){    if(l == r)    {        sum[rt] = 1;        return;    }    int m = (l + r) >> 1;    buil(lson);    buil(rson);    sum[rt] = sum[rt<<1] + sum[rt<<1|1];}int query(int L, int R, int l, int r, int rt){    if(L <= l && r <= R)        return sum[rt];    int m = (l + r) >> 1;    int ret = 0;    if(m >= L) ret += query(L, R, lson);    if(m < R) ret += query(L, R, rson);    return ret;}void update(int p, int l, int r, int rt){    sum[rt]--;    if(l == r)    {        pos = l;        return;    }    int m = (l + r) >> 1;    if(sum[rt<<1] >= p) update(p, lson);    else update(p-sum[rt<<1], rson);}char name[MAXN][15];int a[MAXN];int main(){//    freopen("in.txt", "r", stdin);    while(~scanf("%d%d", &n, &k))    {        for(int i=1; i<=n; i++)            scanf("%s%d", name[i], &a[i]);        mxt = ord = 1;        get(1, 1, 1, 20);        memset(sum, 0, sizeof(sum));        buil(1, n, 1);        update(k, 1, n, 1);        int lft = n - 1;        ord--;        while(ord--)        {            int p = a[pos] % lft;            if(a[pos] < 0) p = ((p + 1) % lft + lft) % lft;            if(p == 0) p = lft;            int lp = query(1, pos, 1, n, 1);            int rp = query(pos, n, 1, n, 1);            if(p <= rp) update(lp+p, 1, n, 1);            else update(p-rp, 1, n, 1);            lft--;        }        printf("%s %I64d\n", name[pos], mxt);    }}